The Golden Number
The Golden Rectangle
The Logarithmic Spiral
The Fibonacci Sequence
The principle exists before the word.
It is through observation and with the help of mathematics that some enlightened humans have managed to identify a constant of proportions ubiquitous in nature and the cosmos.
As logical mathematics is valuable in helping us distinguish right from wrong, logarithmscan help us understand the secrets of beauty.
This key opening the door to what is beautiful is called Divine Proportion, Golden Proportion or Golden Ratio.
Here are some brief concepts and examples of its application in practice.
The Golden Ratio:
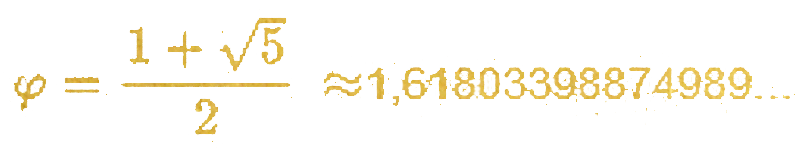
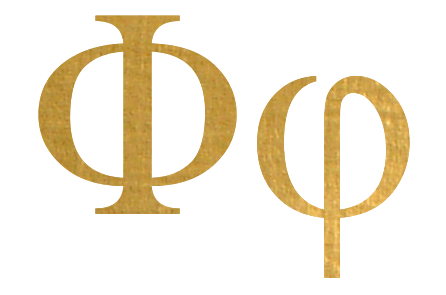
The Greek letter Phi is commonly used to symbolize the Golden Ratio.
Some suggest that the choice of this symbol was made to pay homage to Phidias, a famous ancient sculptor (490 – 430 BC.)
The Golden Ratio is used by artists in search of beauty to balance their compositions and position the center of interest.
The golden number is also known as the “Divine Proportion”, from the title of the book De divina Proportione written by fra Luca Pacioli di Borgo, and illustrated by Leonard de Vinci c. 1498.
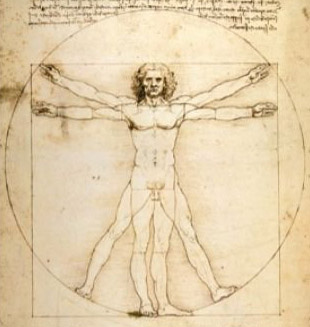
Vitruvian Man by Leonardo da Vinci
The golden number consists of a unique correspondence of numbers in logarithmic mathematics.
The aesthetic emanating from the golden number is perceived as a perfect balance. We find clearly identifiable echoes of this in nature: tree structure, proportions of the human body, growth of the rabbit population (Fibonacci) etc.
The golden number is so in harmony with the laws of nature that artists somewhat sensitive to beauty will unconsciously apply the rules. Are artists not themselves elements of nature?
It is essential that artists initiate themselves to this knowledge, become infused with it and learn to recognize it wherever they look and of course insert it into their work.
The Fibonacci Sequence
Leonardo Fibonacci (c. 1175 in Pisa – c. 1250)
The Fibonacci sequence is a simplified version of the Golden Ratio. It is a series of
numbers in which each term is the sum of the two terms that precede it:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144
The quotients of two consecutive terms of the Fibonacci sequence are the best approximations of the Golden Ratio. Having reached the numbers 89, 144, we obtain an almost perfect match:
89 X 1.618 = 144.002
The correspondence 1, 2 or 1/3 x 2/3, general composition rule, is the ultimate simplification of the Golden Ratio.
The Golden Rectangle and the Logarithmic Spiral:
Golden Rectangle: Rectangle whose longest side is equal to x1.618 the measure of theshortest side. In this rectangle, if you draw a square, the remaining rectangle isproportionally identical to the original rectangle.
Logarithmic Spiral: Trace a square clockwise in each of the remaining rectangles. If youtrace the arc of a circle with a compass inside the squares you will obtain theLogarithmic Spiral.

LOGARITHMIC SPIRAL
EXAMPLES OF THE GOLDEN RATIO IN APPLICATION IN MY COMPOSITIONS
AND RECOGNIZABLE IN THE WORKS OF FAMOUS PAINTERS.
It is easy to see that the Golden Rectangle is rarely used as a format in painting. Despite its undeniable aesthetics, it is not always appropriate depending on the subject you want to paint.
However, it fits usefully inside any form and can thus serve as a guide.
In these two examples of portraits, the model’s left eye – therefore the one on the right – is positioned at the heart of the spiral. The composition in vignette follows the large helix and leads to the signature which in this case is an integral part of the composition.
As you can imagine, the golden number does not always have to be applied to the letter or to the nearest decimal. It would be far too dry and constraining. If nature applied it to its creations with the rigor of a geometrician, the universe would be rigid and monotonous.
Artists build around the golden number by relying on their sensitivity. In this way, they make it subtly but undeniably perceptible and give their compositions a je ne sais quoi that is very pleasing to the eye.
It may even be that by not following the line perfectly, sometimes a little inside, further outside, we manage to create a sensitive vibration of the number that would be very difficult to calculate mathematically. Although, it is quite possible that if we took the trouble to do this infinite calculation we would end up with a perfect match.
Sometimes well hidden and difficult to decode. When the Eye is used, we begin to see it everywhere.

Denis Jacques
Johannie. 2018. Pastel, 23 x 15 in (C.A.)
Annick. 2003. Oil on wood with cotton and gold leaf marouflage, 16 x 12 in (C.A.)
Vu (self-portrait). 2018. Pastel, 18 x 24 in (C.A.)

Phi. Denis Jacques – 2020. Pastel, 24 x 15 in (C.P.) Double spiral

Michelangelo Buonarroti – The Hand of God

The Sabines. Jacques-Louis David. 1799, 385 × 522 cm Paris, Louvre Museum

William A. Bouguereau. Parure des champs 1884. Oil on canvas 162.9 x 89.9 cm
This work is part of the permanent collection of the Montreal Museum of Fine Arts. So within reach. A rare opportunity to see the work of the master of the demi-pâte française.

The golden number appears in the proportions of the regular pentagon, as the ratio between the length of the side of the pentagon and that of the side of the inscribed pentagram.

Leda Atomica. Salvador Dali – 1949. (24.1 in × 17.8 in) (Figueres)
Dali was very interested in the golden number. But we perceive in his “Léda Atomica” that the abuse of calculations can hinder the beauty of the gesture felt.
The Fibonacci series is very useful for placing your subject inside the chosen rectangle, in relation to its edges.

Dagmar. Anders Zorn – 1911. Oil on canvas

Amarti. Denis Jacques – 2021. Oil on wood with cotton marouflage, 20 X 16 in (C.A.)
References :